Exa-MA : Methods and Algorithms for Exascale
Introduction
There is a growing number of problems where experiments are impossible, hazardous, or extremely expensive.
Extreme-scale computing enables the solution of vastly more accurate predictive models and the analysis of massive quantities of data thanks to AI.
Combining predictive modeling with data, coupled with machine learning and AI strategies, can create new opportunities in science. In particular, move from Human-in-the-Loop towards hybrid Human and Artificial Intelligence-driven design, discovery, or evaluation.
However, various scientific and technical challenges need to be met to exploit exascale computing capabilities.
These bottlenecks impact methods and algorithms in a profound way on all aspects of the simulation toolchain through :
- (i) avoidance of communication,
- (ii) adaptive parallel grain and more compute-intensive at node level,
- (iii) handling of heterogeneous hardware and data representations and
- (iv) self-parametrization.
The Exa-MA project aims to push the frontiers of exascale computing by developing cutting-edge numerical methods, algorithms, and software libraries.
- Developing advanced methods tailored for exascale architectures.
- Contributing to open-source software libraries that abstract hardware complexity.
- Integrating AI techniques for simulation, model reduction, and optimization.
- Delivering demonstrators, mini-apps, and proxy apps to validate our approaches.
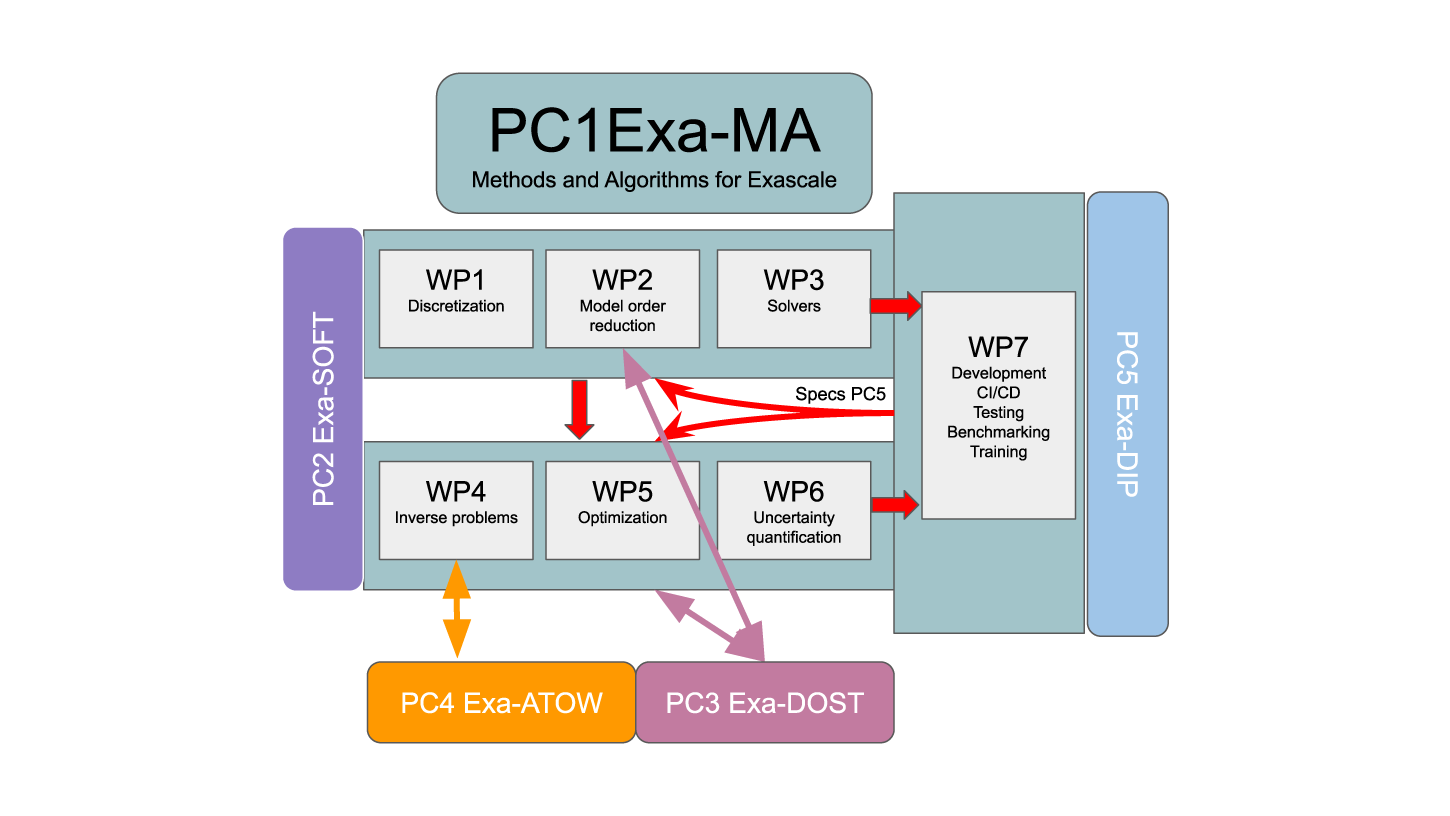
Consortium
Exa-MA is carried out by a consortium of leading institutions:
- CEA
- École Polytechnique
- Inria
- Sorbonne Université
- Université de Strasbourg
Exa-Ma is divided into 7 workpackages (WP), each addressing key aspects of developing methods, algorithms, and software for exascale computing.
Our work packages
Objective
Oversee overall project coordination, scientific and technical management, and administrative tasks.
Key Topics
- Communication and coordination
- Risk and conflict management
- Financial and administrative monitoring
- Governance and compliance
Lead
Université de Strasbourg
Duration
Months 1–60
Description
WP0 establishes the project’s governance structure and ensures smooth operation by integrating contributions from all other work packages. It is responsible for maintaining communication within the consortium, handling administrative duties, and ensuring compliance with funding agreements.
Objective
Develop robust techniques for mesh generation, adaptive refinement, high-order discretization, and efficient time integration for multiphysics simulations.
Key Topics
- Mesh generation (including nonconforming methods)
- Adaptive mesh refinement strategies
- High-order and spectral discretization
- Parallel-in-time and asynchronous time-integration methods
Lead
CEA
Duration
Months 1–60
Description
WP1 focuses on the creation and adaptation of mesh representations and discretization techniques that reduce communication overhead and increase computational intensity—crucial features for exascale applications.
- Objective
Develop fast surrogate models and reduced-order methods by integrating data-driven and physics-based machine learning techniques. - Key Topics
-
- Neural Galerkin methods
- Physics-Informed Neural Networks (PINNs)
- Non-intrusive reduced basis approaches
- Multi-fidelity modeling
- Lead
Inria - Duration
- Months 1–60
- Description
WP2 aims to accelerate simulations by reducing computational complexity while preserving essential features of the physical models. Advanced machine learning tools are leveraged to develop effective surrogate models and reduction techniques.
- Objective
Design scalable solvers for large sparse linear systems and coupled multiphysics problems on exascale architectures. - Key Topics
-
- Domain decomposition methods
- Mixed precision arithmetic and error control
- Adaptive solver strategies
- Robust multiphysics coupling techniques
- Lead
Inria - Duration
Months 1–60 - Description
WP3 focuses on developing robust and efficient solver technologies. The goal is to handle the computational challenges of both mono-physics and coupled multiphysics simulations on modern exascale hardware.
- Objective
Integrate observational data with physical models to solve inverse problems through deterministic and stochastic methods. - Key Topics
-
- Variational and ensemble-based data assimilation
- Stochastic differential equations (SDEs/SPDEs)
- Multi-fidelity strategies for inverse problems
- Optimized observation error models
- Lead
Université de Strasbourg - Duration
Months 1–60 - Description
WP4 addresses the challenge of blending simulation data with real-world observations. Its goal is to improve model predictions and enable enhanced decision-making through advanced data assimilation and inverse problem methodologies.
- Objective
Develop exascale optimization algorithms for tackling combinatorial, continuous, and mixed optimization challenges, including shape optimization and AutoML. - Key Topics
-
- Decomposition-based optimization strategies
- Surrogate-based and multi-fidelity optimization
- Shape optimization techniques
- Optimization for AI (AutoML)
- Lead
Inria - Duration
Months 1–60 - Description
WP5 is dedicated to designing innovative optimization methods that leverage exascale computational capabilities. These methods will facilitate faster and more accurate solutions for complex design, control, and decision-making problems.
- Objective
- Quantify uncertainties in complex multiscale simulations and understand their impact on predictive modeling.
- Key Topics
-
- Kernel-based sensitivity analysis
- Surrogate modeling for uncertainty quantification
- High-dimensional integration and uncertainty propagation
- Multi-arithmetic and multi-fidelity approaches
- Lead
École Polytechnique - Duration
Months 1–60 - Description
WP6 develops techniques to assess and manage uncertainties within simulation models. This work is essential for ensuring that predictions are reliable and for guiding improvements in model fidelity.
- Objective
Coordinate the integration, testing, and benchmarking of methods and software developed across the Exa-MA project, ensuring interoperability and high performance. - Key Topics
-
- Development of benchmarking frameworks and non-regression tests
- Creation of demonstrators, mini-apps, and proxy-apps
- Training and dissemination activities
- Agile co-design and continuous integration
- Lead
Université de Strasbourg - Duration
Months 1–60 - Description
WP7 acts as the central hub for evaluating and validating the project’s outputs. It provides a structured environment for testing, benchmarking, and training, ensuring that all developed components work cohesively on exascale architectures.
Software
The Work Package 7 (WP7) in the Exa-MA project focuses on several key objectives. Firstly, it involves software development ranging from basic to advanced testing, including benchmarking, to verify the capabilities of exascale computing and address identified challenges. The aim is to deliver software packages following the continuous integration/continuous delivery (CI/CD) framework proposed by ExaDIP. Secondly, WP7 coordinates co-design activities within Exa-MA, working closely with the ExaDIP project. This collaboration ensures effective communication and synergy between the projects to drive advancements in exascale computing.
Additionally, WP7 aims to establish a showroom to showcase the results achieved through Exa-MA. This showroom will serve as a platform to present and highlight the outcomes and achievements of the project.
Lastly, WP7 contributes to the creation of training material based on the results of Exa-MA. The insights gained from the project will be leveraged to develop educational resources and materials, facilitating knowledge transfer and dissemination.
To accomplish these objectives, WP7 relies on the principles of non-regression, verification, and validation. The various studies and developments conducted across different work packages within Exa-MA will undergo rigorous testing and evaluation before integration into a demonstrator.
WP7 is staffed by a dedicated team of engineers who work at the intersection of Exa-MA and other projects, particularly ExaDIP. The management of WP7 follows an Agile approach, aligning with the project management plan established in WP0 to ensure efficient and effective progress towards the set goals.
Our software
Arcane is a development environment for parallel numerical calculation codes. It supports the architectural aspects of a calculation code, such as data structures for meshing and parallelism, as well as more environment-related aspects such as dataset configuration.
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
Packages exist
✓
Packages published in repos
|
Unit test exist ✓ CI exist✓ CI runs regularly (each new release)✓ CI runs regularly (each commit) |
Publicly available source repository ✓ Supports contribution via pull requestsRepository: github.com/arcaneframework/framework |
License clearly stated ✓ FLOSS license (FSF/OSI conformant)✓ SPDX is used✓ REUSE is used |
Documentation exists ✓ Easily browsable online |
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
Channel exists
✓
Freely joinable without invitation
|
Software name ✓ Description✓ License✓ Documentation URL✓ Discussion channel URL✓ Package repositories URLs✓ Repository URL✓ Autoevaluation using the list of criteria stated here |
API changes documented ✓ Semantic Versioning used✓ Clear release policy |
Tests exist ✓ Scripts to automate tests on supercomputers✓ Scripts/tools easing portability to new hardware |
CGAL is a software project that provides easy access to efficient and reliable geometric algorithms in the form of a C++ library.
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
Spack: github.com/spack/spack
Also available on: Debian, Ubuntu, Fedora, Spack |
|
Repository: github.com/CGAL |
|
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
Aucun canal public identifié
|
|
|
|
Composyx is a linear algebra C++ library focused on composability. Its purpose is to allow the user to express a large pannel of algorithms using a high-level interface to range from laptop prototypes to many node supercomputer parallel computations.
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
✓
Packages exist
✓
Packages published in repos
Packages installation tested on supercomputers
✓
Packages available in community repositories
Disponible dans GUIX-HPC
|
Unit test exist
✓
CI exist
✓
CI runs regularly (each new release)
CI runs regularly (each commit)
|
✓
Publicly available source repository
✓
Supports contribution via pull requests
Repository: gitlab.inria.fr/composyx/composyx |
✓
License clearly stated
FLOSS license (FSF/OSI conformant)
SPDX is used
REUSE is used
|
✓
Documentation exists
Easily browsable online
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
✓
Channel exists
✓
Freely joinable without invitation
Aucun canal public identifié
|
✓
Software name
Description
✓
License
Documentation URL
Discussion channel URL
✓
Package repositories URLs
✓
Repository URL
✓
Autoevaluation using the list of criteria stated here
|
API changes documented
Semantic Versioning used
Clear release policy
|
✓
Tests exist
Scripts to automate tests on supercomputers
Scripts/tools easing portability to new hardware
|
Versatile and flexible numerical library that implements Block Krylov iterative schemes for the solution of linear systems of equations with multiple right-hand sides
This Library currently implements various variants of Block Krylov iterative solvers:
- BCG (Block Conjugate Gradient)
- BF-BCG (Breadown Free BCG)
- BGCR (Block Generalized Conjugate Residual)
- BGMRES (Block General Minimum Residual)
- IB-BGMRES (BGMRES with inexact breakdown)
- BGMRES-DR (BGMRES with deflated restarting)
- IB-BGMRES-DR (BGMRES with inexact breakdown and deflated restarting)
- IB-BGCRO-DR (Block Generalized Conjugate Residual Method with Inner Orthogonalization with inexact breakdown and deflated restarting)
A particular attention is paid to internal numerical kernels such as those associated with the least-square solution where block Incremental QR factorization variants are implemented.
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
✓
Packages exist
✓
Packages published in repos
Packages installation tested on supercomputers
✓
Packages available in community repositories
Disponible dans GUIX-HPC
|
Unit test exist
✓
CI exist
CI runs regularly (each new release)
CI runs regularly (each commit)
|
✓
Publicly available source repository
✓
Supports contribution via pull requests
Repository: gitlab.inria.fr/solverstack/fabulous |
✓
License clearly stated
FLOSS license (FSF/OSI conformant)
SPDX is used
REUSE is used
|
✓
Documentation exists
Easily browsable online
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
✓
Channel exists
✓
Freely joinable without invitation
Aucun canal public identifié
|
✓
Software name
Description
✓
License
Documentation URL
Discussion channel URL
✓
Package repositories URLs
✓
Repository URL
✓
Autoevaluation using the list of criteria stated here
|
API changes documented
Semantic Versioning used
Clear release policy
|
✓
Tests exist
Scripts to automate tests on supercomputers
Scripts/tools easing portability to new hardware
|
Feel is an open-source, high-performance C framework for solving complex PDE and ODE-based mathematical models using advanced Galerkin methods (finite element, discontinuous Galerkin, and spectral methods) and efficient reduced-order modeling (ROM) techniques, including Reduced Basis (RB), Proper Orthogonal Decomposition (POD), and Empirical Interpolation Methods (EIM). It features specialized application toolboxes (CFD, CSM, FSI, thermoelectric, Maxwell), modern parallel computing with seamless Python integration (Pybind11), and extensive DevOps support (CI/CD, benchmarking, and containers). Feel++ is used in academia and industry for multiphysics simulations, inverse problems, uncertainty quantification, data assimilation, and machine learning applications.
Download Feel++ :
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
✓
Packages exist
✓
Packages published in repos
Packages installation tested on supercomputers
✓
Packages available in community repositories
Spack: numpex/spack.numpex
Guix: guix-hpc Docker / Apptainer: Feel++ containers Disponible sur : Debian, Ubuntu, Fedora, Spack, GUIX-HPC |
✓
Unit test exist
✓
CI exist
✓
CI runs regularly (each new release)
✓
CI runs regularly (each commit)
|
✓
Publicly available source repository
✓
Supports contribution via pull requests
Repository: github.com/feelpp/feelpp |
✓
License clearly stated
✓
FLOSS license (FSF/OSI conformant)
SPDX is used
REUSE is used
|
✓
Documentation exists
✓
Easily browsable online
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
✓
Channel exists
✓
Freely joinable without invitation
|
✓
Software name
✓
Description
✓
License
✓
Documentation URL
✓
Discussion channel URL
✓
Package repositories URLs
✓
Repository URL
✓
Autoevaluation using the list of criteria stated here
|
✓
API changes documented
✓
Semantic Versioning used
Clear release policy
|
✓
Tests exist
✓
Scripts to automate tests on supercomputers
Scripts/tools easing portability to new hardware
|
FreeFEM is a partial differential equation solver for non-linear multi-physics systems in 2D and 3D using the finite element method.
Problems involving partial differential equations from several branches of physics such as fluid-structure interactions require interpolations of data on several meshes and their manipulation within one program.
FreeFEM includes a fast interpolation algorithm and a language for the manipulation of data on multiple meshes. It is written in C++ and the FreeFEM language is a C++ idiom.
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
✓ Packages exist✓ Packages published in reposPackages installation tested on supercomputers ✓ Packages available in community repositories
Spack: spack/spack
Disponible sur : Debian, Spack |
✓ Unit test exist✓ CI existCI runs regularly (each new release) CI runs regularly (each commit)
|
✓ Publicly available source repository✓ Supports contribution via pull requestsRepository: github.com/FreeFem/FreeFem-sources |
✓ License clearly stated✓ FLOSS license (FSF/OSI conformant)SPDX is used REUSE is used
|
✓ Documentation existsEasily browsable online non disponible
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
✓ Channel exists✓ Freely joinable without invitationnon disponible
|
✓ Software nameDescription ✓ LicenseDocumentation URL Discussion channel URL ✓ Package repositories URLs✓ Repository URL✓ Autoevaluation using the list of criteria stated here |
✓ API changes documented✓ Semantic Versioning used✓ Clear release policy |
✓ Tests existScripts to automate tests on supercomputers Scripts/tools easing portability to new hardware
|
Hawen solves time-harmonic wave problems for acoustic and elastic media using the Hybridizable Discontinuous Galerkin (HDG) method for discretization. It combines mpi and OpenMP parallelism to solve large-scale applications such as Earth’s imaging and helioseismology.
It can handle the forward problem (propagation of waves) as well as the inverse problem (parameter identification).
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
✓ Packages exist✓ Packages published in reposPackages installation tested on supercomputers ✓ Packages available in community repositoriesDisponible sur : GUIX-HPC
|
Unit test exist CI exist CI runs regularly (each new release) CI runs regularly (each commit)
|
✓ Publicly available source repository✓ Supports contribution via pull requestsRepository: gitlab.com/ffaucher/hawen |
✓ License clearly stated✓ FLOSS license (FSF/OSI conformant)SPDX is used REUSE is used Licence : GPL v*
|
✓ Documentation existsEasily browsable online non disponible
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
✓ Channel exists✓ Freely joinable without invitationnon disponible
|
✓ Software nameDescription ✓ LicenseDocumentation URL Discussion channel URL ✓ Package repositories URLs✓ Repository URL✓ Autoevaluation using the list of criteria stated here |
API changes documented Semantic Versioning used Clear release policy
|
✓ Tests existScripts to automate tests on supercomputers Scripts/tools easing portability to new hardware
|
HPDDM is an efficient implementation of various domain decomposition methods (DDM) such as one- and two-level Restricted Additive Schwarz (RAS) methods, the Finite Element Tearing and Interconnecting (FETI) method, and the Balancing Domain Decomposition (BDD) method.
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
✓ Packages exist✓ Packages published in reposPackages installation tested on supercomputers ✓ Packages available in community repositoriesDisponible via Spack : hpddm/package.py
|
✓ Unit test exist✓ CI existCI runs regularly (each new release) CI runs regularly (each commit)
|
✓ Publicly available source repository✓ Supports contribution via pull requestsRepository: github.com/hpddm/hpddm |
✓ License clearly stated✓ FLOSS license (FSF/OSI conformant)SPDX is used REUSE is used Licence : LGPL v*
|
✓ Documentation existsEasily browsable online non disponible
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
✓ Channel exists✓ Freely joinable without invitationnon disponible
|
✓ Software nameDescription ✓ LicenseDocumentation URL Discussion channel URL ✓ Package repositories URLs✓ Repository URL✓ Autoevaluation using the list of criteria stated here |
API changes documented Semantic Versioning used Clear release policy
|
✓ Tests existScripts to automate tests on supercomputers Scripts/tools easing portability to new hardware
|
MaHyCo is a inite volume code for solving hydrodynamic equations: Lagrangian or Eulerian simulations.
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
Packages exist Packages published in repos Packages installation tested on supercomputers Packages available in community repositories
|
Unit test exist ✓ CI existCI runs regularly (each new release) ✓ CI runs regularly (each commit) |
✓ Publicly available source repository✓ Supports contribution via pull requestsRepository: github.com/cea-hpc/MaHyCo |
✓ License clearly statedFLOSS license (FSF/OSI conformant) SPDX is used REUSE is used Licence : Apache-2.0
|
✓ Documentation existsEasily browsable online non disponible
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
✓ Channel exists✓ Freely joinable without invitationnon disponible
|
✓ Software nameDescription ✓ LicenseDocumentation URL Discussion channel URL ✓ Package repositories URLs✓ Repository URL✓ Autoevaluation using the list of criteria stated here |
API changes documented Semantic Versioning used Clear release policy
|
Tests exist Scripts to automate tests on supercomputers Scripts/tools easing portability to new hardware
|
MUMPS is a high-performance software package for solving large sparse linear systems, supporting a wide range of matrix types and arithmetic precisions, with advanced features like parallel processing, iterative refinement, out-of-core computation, and interfaces for Fortran, C, Matlab, and Scilab.
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
✓ Packages exist✓ Packages published in reposPackages installation tested on supercomputers ✓ Packages available in community repositoriesSpack, PETSc
|
Unit test exist CI exist CI runs regularly (each new release) CI runs regularly (each commit)
|
✓ Publicly available source repositorySupports contribution via pull requests Repository: mumps-solver.org |
✓ License clearly statedFLOSS license (FSF/OSI conformant) SPDX is used REUSE is used Licence : CeCILL
|
✓ Documentation existsEasily browsable online non disponible
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
✓ Channel exists✓ Freely joinable without invitationnon disponible
|
✓ Software nameDescription ✓ LicenseDocumentation URL Discussion channel URL ✓ Package repositories URLs✓ Repository URL✓ Autoevaluation using the list of criteria stated here |
API changes documented Semantic Versioning used Clear release policy
|
Tests exist Scripts to automate tests on supercomputers Scripts/tools easing portability to new hardware
|
PaStiX (Parallel Sparse matriX package) is a scientific library that provides a high performance parallel solver for very large sparse linear systems based on direct methods. Numerical algorithms are implemented in single or double precision (real or complex) using LLt, LDLt and LU with static pivoting (for non symmetric matrices having a symmetric pattern). This solver also provides some low-rank compression methods to reduce the memory footprint and/or the time-to-solution.
To know more about this software, please contact Christophe Prud’homme
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
✓ Packages exist✓ Packages published in reposPackages installation tested on supercomputers ✓ Packages available in community repositories
Available packages: GUIX-HPC, PETSc
|
Unit test exist CI exist CI runs regularly (each new release) CI runs regularly (each commit)
|
✓ Publicly available source repositorySupports contribution via pull requests Repository: nan |
✓ License clearly statedFLOSS license (FSF/OSI conformant) SPDX is used REUSE is used
|
✓ Documentation existsEasily browsable online
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
Channel exists Freely joinable without invitation |
✓ Software nameDescription ✓ LicenseDocumentation URL Discussion channel URL ✓ Package repositories URLsRepository URL ✓ Autoevaluation using the list of criteria stated here |
API changes documented Semantic Versioning used Clear release policy
|
✓ Tests existScripts to automate tests on supercomputers Scripts/tools easing portability to new hardware
|
PETSc, the Portable, Extensible Toolkit for Scientific Computation, pronounced PET-see, is for the scalable (parallel) solution of scientific applications modeled by partial differential equations (PDEs).
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
✓ Packages exist✓ Packages published in reposPackages installation tested on supercomputers ✓ Packages available in community repositories
Available packages:
Debian, Ubuntu, Fedora, Other, Spack (github.com/spack/spack) |
✓ Unit test exist✓ CI existCI runs regularly (each new release) ✓ CI runs regularly (each commit) |
✓ Publicly available source repositorySupports contribution via pull requests Repository: nan |
✓ License clearly statedFLOSS license (FSF/OSI conformant) SPDX is used REUSE is used
|
✓ Documentation existsEasily browsable online
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
✓ Channel exists✓ Freely joinable without invitation |
✓ Software nameDescription ✓ LicenseDocumentation URL Discussion channel URL ✓ Package repositories URLsRepository URL ✓ Autoevaluation using the list of criteria stated here |
API changes documented Semantic Versioning used Clear release policy
|
✓ Tests existScripts to automate tests on supercomputers Scripts/tools easing portability to new hardware
|
Qr_mumps is a software package for the solution of sparse, linear systems on multicore computers. It implements a direct solution method based on the QR factorization of the input matrix. Therefore, it is suited to solving sparse least-squares problems and to computing the minimum-norm solution of sparse, underdetermined problems. It can obviously be used for solving square problems in which case the stability provided by the use of orthogonal transformations comes at the cost of a higher operation count with respect to solvers based on, e.g., the LU factorization. Qr_mumps supports real and complex, single or double precision arithmetic.
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
✓ Packages exist✓ Packages published in reposPackages installation tested on supercomputers ✓ Packages available in community repositories
Available packages:
GUIX-HPC |
Unit test exist ✓ CI exist✓ CI runs regularly (each new release)CI runs regularly (each commit)
|
✓ Publicly available source repository✓ Supports contribution via pull requestsRepository: gitlab.com/qr_mumps/qr_mumps |
✓ License clearly statedFLOSS license (FSF/OSI conformant) SPDX is used REUSE is used
|
✓ Documentation existsEasily browsable online
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
✓ Channel exists✓ Freely joinable without invitation |
✓ Software nameDescription ✓ LicenseDocumentation URL Discussion channel URL ✓ Package repositories URLs✓ Repository URL✓ Autoevaluation using the list of criteria stated here |
API changes documented Semantic Versioning used Clear release policy
|
✓ Tests existScripts to automate tests on supercomputers Scripts/tools easing portability to new hardware
|
The use of mesh adaptation methods in numerical simulation allows to drastically reduce the memory footprint and the computational costs. There are different kinds of methods: AMR patch-based, AMR cell-based, multiresolution cell-based or point-based, …
Different open source software is available to the community to manage mesh adaptation: AMReX for patch-based AMR, p4est and pablo for cell-based adaptation.
The strength of samurai is that it allows to implement all the above mentioned mesh adaptation methods from the same data structure. The mesh is represented as intervals and a set algebra allows to efficiently search for subsets among these intervals. Samurai also offers a flexible and pleasant interface to easily implement numerical methods.
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
✓ Packages existPackages published in easily usable repositories Packages installation tested on supercomputers Packages available in community repositories |
✓ Unit tests exist✓ CI exists✓ CI runs regularly (each new release)✓ CI runs regularly (each commit) |
✓ Publicly available source repository✓ Supports contribution via pull requestsRepository: github.com/hpc-maths/samurai |
✓ License clearly stated✓ FLOSS license (FSF/OSI conformant)SPDX is used REUSE is used ✓ OSS: BSD |
✓ Documentation existsEasily browsable online
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
✓ Channel exists✓ Freely joinable without invitation |
✓ Software nameDescription ✓ LicenseDocumentation URL Discussion channel URL ✓ Package repositories URLs✓ Repository URL✓ Autoevaluation using criteria list |
API changes documented Semantic Versioning used Clear release policy
|
✓ Tests existScripts to automate tests on supercomputers Scripts/tools easing portability to new hardware
|
TRUST is a thermalhydraulic software package for CFD simulations. This software was originally designed for conduction, incompressible single-phase, and Low Mach Number (LMN) flows with a robust Weakly-Compressible (WC) multi-species solver. However, a huge effort has been conducted recently, and now TRUST is able to simulate real compressible multi-phase flows.
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
Packages exist Packages published in repos Packages installation tested on supercomputers Packages available in community repositories
|
✓ Unit test exist✓ CI existCI runs regularly (each new release) ✓ CI runs regularly (each commit) |
✓ Publicly available source repository✓ Supports contribution via pull requestsRepository: github.com/cea-trust-platform |
✓ License clearly stated✓ FLOSS license (FSF/OSI conformant)SPDX is used REUSE is used
|
✓ Documentation existsEasily browsable online
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
✓ Channel exists✓ Freely joinable without invitation |
✓ Software nameDescription ✓ LicenseDocumentation URL Discussion channel URL ✓ Package repositories URLs✓ Repository URL✓ Autoevaluation using the list of criteria stated here |
API changes documented Semantic Versioning used Clear release policy
|
✓ Tests exist✓ Scripts to automate tests on supercomputersScripts/tools easing portability to new hardware
|
The Uranie platform is an open-source framework developed at the Alternative Energies and Atomic Energy Commission (CEA), in the nuclear energy division, in order to deal with uncertainty propagation, surrogate models, optimisation issues, code calibration, etc. This platform benefits from both its dependencies and from personal developments, to offer an efficient data handling model, a C++ and Python interface, advanced graphi graphical tools, several parallelisation solutions, etc. These methods can then be applied to many kinds of code (considered as black boxes by Uranie) so to many fields of physics as well.
| Packaging | Minimal Validation Tests | Public Repository | Clearly-identified license | Minimal Documentation |
|---|---|---|---|---|
|
Packages exist
Packages published in easily usable repositories
Packages installation tested on supercomputers
Packages available in community repositories
|
✓ Unit test exist✓ CI existCI runs regularly (each new release)
✓ CI runs regularly (each commit) |
✓ Publicly available source repositorySupports contribution via pull requests
Repository: uranie.cea.fr
|
✓ License clearly stated✓ FLOSS license (FSF/OSI conformant)SPDX is used
REUSE is used
|
✓ Documentation existsEasily browsable online
|
| Open Public Discussion Channel | Metadata | API Compatibility Information | Minimal Performance Tests |
|---|---|---|---|
|
✓ Channel exists✓ Freely joinable without invitation |
✓ Software name✓ Description✓ License✓ Documentation URL✓ Discussion channel URL✓ Package repositories URLs✓ Repository URL✓ Autoevaluation using the list of criteria stated here |
API changes documented
Semantic Versioning used
Clear release policy
|
✓ Tests existScripts to automate tests on supercomputers
Scripts/tools easing portability to new hardware
|
Save the Date
Exa-MA events
Discover the next Exa-MA events: our seminars and conferences, as well as partner events
february, 2026
News
Exa-MA latest news
The Team
The Exa-MA Team
Discover the members
Contact Us
Stay in contact with Exa-MA
Leave us a message, we will contact you as soon as possible